[SPI・数学]組み合わせ:重複[無料問題集]

今回はSPIの重複組み合わせ問題について確認していきましょう。


SPI重複の例題
重複の問題は\(\frac{r!}{a!b!c!}\)の公式を用いて計算します。
公式を使えば一瞬で答えを求められますが、どうしてそのような公式になるのか、この問題を通して理解していきましょう。
問題1-1
去年は旅行でアメリカに3回、イギリスに2回、中国に1回訪れた。
訪れた順番は[]通り考えられる。
(ログイン後回答すると、ここに前回の正誤情報が表示されます)

問題2-1
下図のような市外路において、AからBへ行く方法を考える。
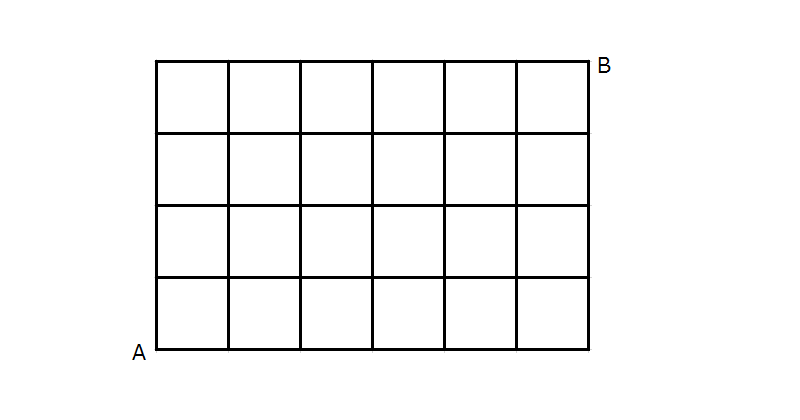
最短のルートは[]通り考えられる。
(ログイン後回答すると、ここに前回の正誤情報が表示されます)
SPI重複のまとめ
この他にも重複組み合わせの問題はいくつかパターンがあります。
しかし、どのような場合でも先程の公式\(\frac{r!}{a!b!c!}\)を用いれば解けるので、問題を解いてしっかり押さえていきましょう


福井県産。北海道に行ったり新潟に行ったりと、雪国を旅してます。
経理4年/インフラエンジニア7年(内4年は兼務)/ライター5年(副業)
簿記2級/FP2級/応用情報技術者/情報処理安全確保支援士/中小企業診断修得者 など





ディスカッション
コメント一覧
まだ、コメントがありません