[SPI・数学]集合：差集合[無料問題集]
今回はSPIにおける差集合の問題を確認していきましょう。
SPI差集合の例題
今回はSPIの差集合を扱う問題です。
他の集合問題同様、ベン図を使って解いていきましょう！
問
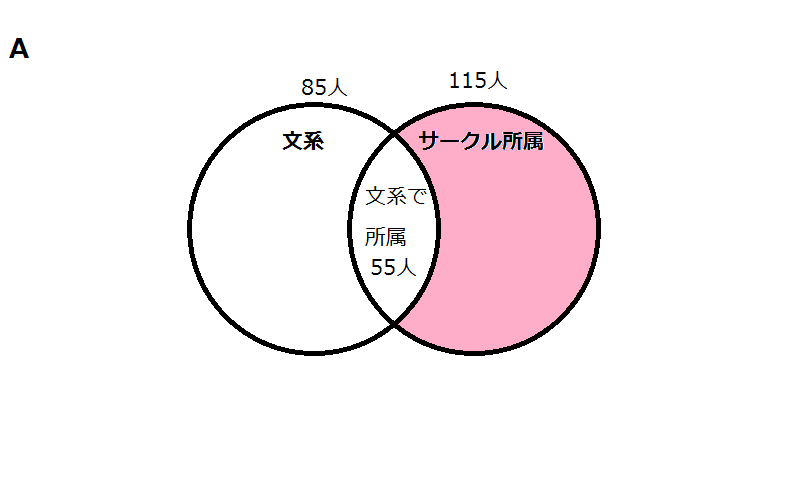
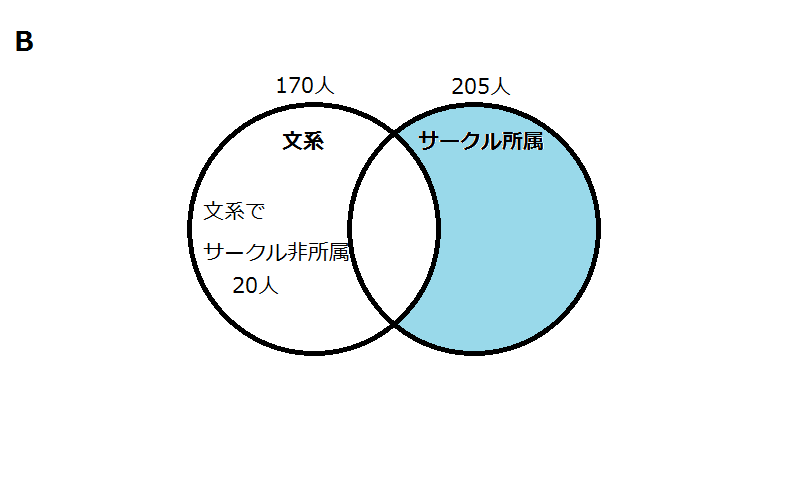
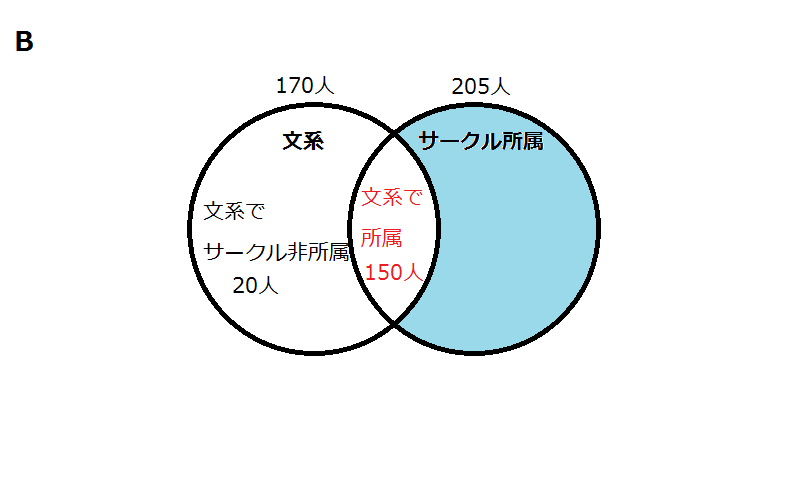
ある大学A、Bの各学生250人ずつ、合計500人にそれぞれ、文系か理系かを尋ね、また、サークルに所属しているか否かの質問をした。下表はその結果をまとめたものである。
| 質問内容 | 回答 | A | B |
| 文系or理系 | 文系 | 85 | 170 |
| 理系 | 165 | 80 | |
| サークルに所属しているか | している | 115 | 205 |
| していない | 135 | 45 |
文系でサークルに所属している大学Aの学生は55人、文系でサークルに所属していないBの学生は20人だった。このとき、理系でサークルに所属している学生は両方の大学あわせて何人か。
人
(ログイン後回答すると、ここに前回の正誤情報が表示されます)
それぞれのベン図の、左の円の内側が文系、右の円の内側がサークルに所属しているとします。
A
まずはAから見ていきましょう。
問われているのは理系でサークルに所属している人数、つまり、色が塗られているところになります。
サークルに所属している人数は115人、その中で文系は55人いることが分かります。
よって理系でサークルに所属している人数を求める式は以下のようになります。
\[115 \verb|(人)| – 55 \verb|(人)| = 60 \verb|(人)|\]
よって60人となります。
B
次にBです。
文系でサークル非所属の人数は20人と分かっていますが、ここから一気に理系でサークルに属している人を求めることはできません。
まずは文系でサークルに所属している人数を求めます。
文系全体で170人いて、そのうち20人がサークルに所属していないので、残りの150人がサークルに所属していることになります。
ここから理系でサークルに所属している人数を求めると、以下のようになります。
\[205 \verb|(人)| – 150 \verb|(人)| = 55 \verb|(人)|\]
したがって文系は、55人となります。
問題文では両方の大学の理系かつサークルに所属している人数を求めているので、それぞれの人数を足し合わせます。
\[60 \verb|(人)| + 55 \verb|(人)| = 115 \verb|(人)|\]
理系でサークルに所属している学生は両方の大学あわせてより、115人が答えとなります。
SPI差集合のまとめ
今回のように、集合が二つある場合はベン図を複数書いて、それぞれの集合に分けることで、状況を整理することができます。
福井県産。北海道に行ったり新潟に行ったりと、雪国を旅してます。
経理4年/インフラエンジニア7年(内4年は兼務)/ライター5年(副業)
簿記2級/FP2級/応用情報技術者/情報処理安全確保支援士/中小企業診断修得者 など
