[SPI・数学]集合：排他的論理和[無料問題集]
今回はSPIにおける排他的論理和の問題を確認していきましょう。
SPI排他的論理和の例題
今回はSPIの排他的論理和を扱う問題です。
難しい名前ですが、要するにダブっていない場所だけを求める問題です。
ベン図やカルノー図を使うとあっという間に解けてしまいます。
問題
とあるゲーム会社P社はソフトS及びMを発売した。このソフトS、Mそれぞれについて、「価格」と「内容」がそれぞれ満足か不満足かのアンケートを500人を対象に行ったところ、結果は下表の通りとなった。
| 項目 | 満足 | 不満足 | |
| S | 価格 | 350 | 150 |
| 内容 | 400 | 100 | |
| M | 価格 | 300 | 200 |
| 内容 | 450 | 50 |
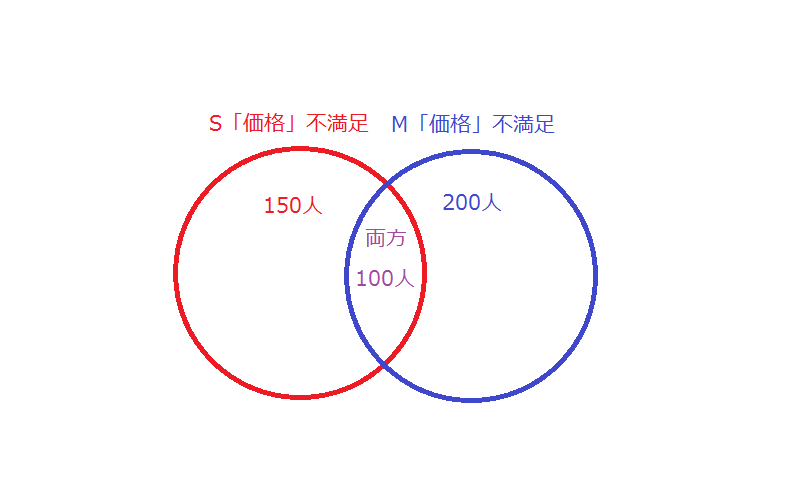
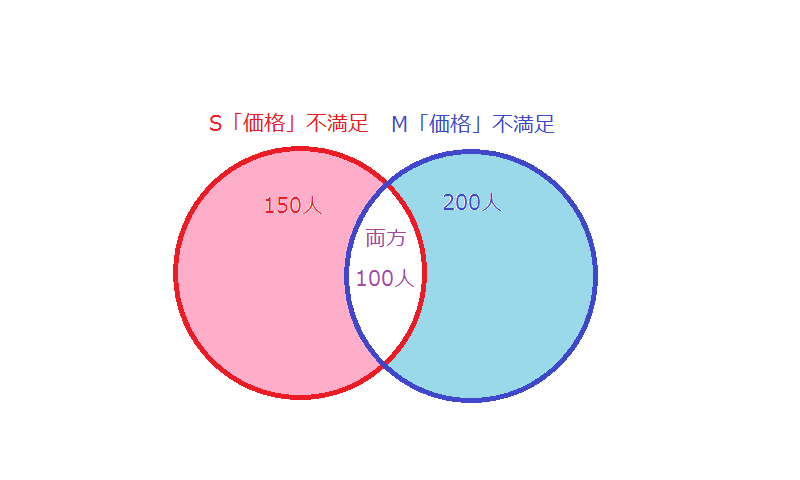
「価格」について、ソフトSもソフトMも不満足と答えた人が100人いた。このとき、ソフトSかソフトMのいずれか一方だけ「価格」が満足と答えた人は何人いるか。
人
(ログイン後回答すると、ここに前回の正誤情報が表示されます)
ここで求めたい人数は、ソフトSかソフトMのいずれか一方だけ「価格」が満足と答えた人でした。
この図だけでは不満足の人数しか分からないため、「価格」に対してソフトSかソフトMのいずれか一方だけ満足した人の人数が分からないかと思いがちです。
しかし言い換えると、ソフトSかソフトMのいずれか一方だけ「価格」が不満足と答えた人の数と同じ意味になります。よって下図の塗りつぶしたところを求めれば良いのです。
色つきの部分を求めるには、それぞれの人数を足して、重なっているところを2回引く(1回引いただけでは和集合を求めることになってしまうため)ことで求められるので、式は以下のようになります。
\[150 \verb|(人)| + 200 \verb|(人)| – 100 \verb|(人)| – 100 \verb|(人)| \\ = 150 \verb|(人)|\]
したがって、正解は150人です。
SPI排他的論理和のまとめ
問題のように、どちらか片一方のみに属している集合のことを、排他的論理和(XOR)と呼びます。
この排他的論理和はSPIの試験だけでなく、あらゆる場面(電子回路やエクセル等)で使うので、是非覚えておきましょう。
福井県産。北海道に行ったり新潟に行ったりと、雪国を旅してます。
経理4年/インフラエンジニア7年(内4年は兼務)/ライター5年(副業)
簿記2級/FP2級/応用情報技術者/情報処理安全確保支援士/中小企業診断修得者 など
