[情報処理技術者試験]2進数・10進数・16進数の意味と進数変換の方法

人は生活上、10進数に慣れていますが、コンピュータが扱う進数は2進数です。

進数違いを理解し、進数変換の方法を理解しなければ、情報処理試験をはじめいたるところで苦戦します。

記事では進数の意味や計算の手順について解説します。

10進数とは

10進数は、普段私達が使っている進数で非常に馴染み深い数です。10進数を2進数・16進数などに進数変換する場合、あらためて10進数を理解する必要があります。

10進数の桁上がり

10進数の場合、数字を$0、1、2、・・・7、8、9$と数えていくと$9$の次に桁が上がって$10$になります。

そして$10、11、12、・・・97、98、99$と数えていくと$99$の次に桁が上がり$100$になります。

この$1$が$10$個集まって$10$になったときは$10$が$1$回ということで、$10^{1}$、$10$が$10$個集まって$100$になったときは$10$を$2$回かけた塊として、$10^{2}$のように表します。

このように、数字が$10$個集まって桁が一つ上がることを$10$を基数にしていると言います。

分かりやすい例で挙げると、$2023$の場合、$10^{3}$が$2$個、$10^{2}$が$0$個、$10^{1}$が$2$個、$10^{0}$が$3$個集まったものと考えられます。

2進数・16進数について

次に少し馴染みにくい進数の2進数・16進数についても確認しましょう。

• 2進数
• 16進数
• その他の進数

2進数

2進数はその名の通り、「$0$」と「$1$」の2つの数字だけを扱います。

$0$の次は$1$になりますが、$1$の次は$2$ではなく、桁が上がって$10$となります。。

このように$2$を基数としたものを2進数と呼び、2倍ごとに桁が上がっていきます。

例を挙げるなら$10010$であれば、$2^{4}$が$1$個、$2^{3}$が$0$個、$2^{2}$が$0$個、$2^{1}$が$1$個、$2^{0}$が$0$個集まったものと考えられます。

10進数と2進数の対応表は以下のようになります。

10進数	0	1	2	3	4	5	6	7
2進数	0	1	10	11	100	101	110	111

10進数	8	9	10	11	12	13	14	15
2進数	1000	1001	1010	1011	1100	1101	1110	1111

16進数

16進数は$16$を基数として数える方法です。数字では$0$から$9$までしか扱えないので、それに加えて$A$から$F$の6つのアルファベットを加えて$16$の数字を活用します。

$9$の次が$10$にならずに$A、B、・・・$と増えて行き、$F$の次に初めて$10$となります。

それ以降も同様で、$9F$の次が$100$になるのではなく、$FF$の次が$100$になる点も注意しましょう。

10進数と16進数の対応表は以下になります。

10進数	0	1	2	3	4	5	6	7
16進数	0	1	2	3	4	5	6	7

(10)	8	9	10	11	12	13	14	15	16
(16)	8	9	A	B	C	D	E	F	10

その他の進数

2進数や16進数以外にも、身の回りにはいくつもの進数が存在しています。

例えば$1$日は$24$時間なので時間は24進数です。$1$時間は$60$分なので分は60進数と考えられます。

ただし、2進数・16進数以外はあまり情報処理技術者試験で問われることが無いので割愛します。

進数変換の計算方法

次に進数の変換・計算方法を確認しましょう。

• n進数から10進数
• 10進数からn進数

n進数から10進数

まずはn進数(今回の場合だとnには2や16が入る)から10進数へ変換する方法から確認しましょう。

$n$は自然数(Natural number)の頭文字で、任意の自然数を入れて良いです。

$n$進数の場合、各桁に$n$個の塊がいくつあるかを見ていくことになります。

10101がn進数の場合は$n^{4}$が$1$個、$n^{3}$が$0$個、$n^{2}$が$1$個、$n^{1}$が$0$個、$n^{0}$が$1$個集まった数字です。

具体的にnに値を放り込んで計算しましょう。

10101が2進数だとすると、10進数で表した場合は$2^{4}$が$1$個、$2^{3}$が$0$個、$2^{2}$が$1$個、$2^{1}$が$0$個、$2^{0}$が$1$個なので、以下のようになります。

次に10101が16進数だとすると、10進数で表した場合は$16^{4}$が$1$個、$16^{3}$が$0$個、$16^{2}$が$1$個、$16^{1}$が$0$個、$16^{0}$が$1$個なので、以下のようになります。

同じような要領で$n$に任意の数字を代入すればその進数を10進数に変換したときの値をがすぐに求まります。

10進数からn進数

次に10進数をn進数に変換する方法です。

こちらは10進数の中にいくつnの塊を作ることができるか考える必要があります。つまり$n$で割っていけば良いです。

そしてもう一つ着眼すべきは余りです。

求め方としては元の10進数$D$を$n$で割り、商を$a_{1}$、余りを$b_{1}$。次に商の$a_{1}$を再び$n$で割り、商を$a_{2}$、余りを$b_{2}$としてその作業を商の値が$n$の値より小さくなるまで続けます。

図に描くと以下のようになります。

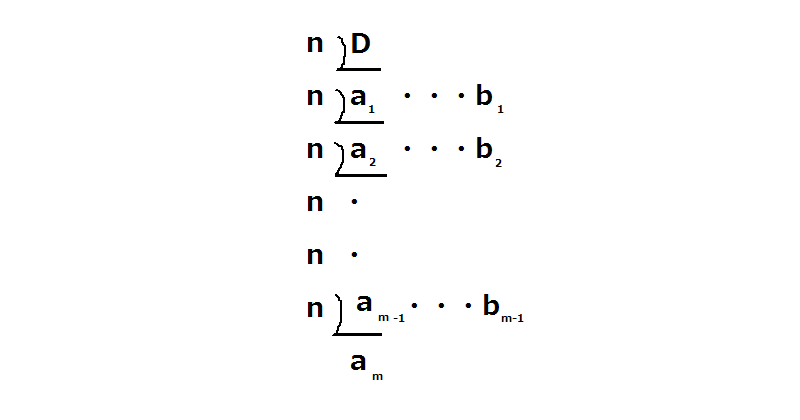
そしてこれを$a_{m}$から図のように羅列します。

$a_{m}b_{m-1}･･･b_{2}b_{1}$が10進数に変換した値になります。これだけだと分かりづらいので、具体的な数字を入れてみましょう。

10進数の数字を$1000$として、これを16進数に変換する流れを見ていきます。

上の図の$D$に$1000$を、$n$に$16$を代入します。結果以下のようになります。

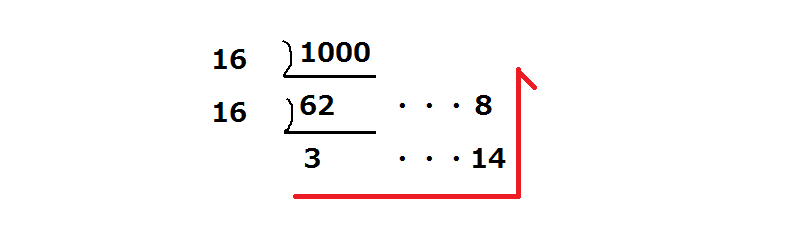
数字を矢印の方向に読めばいいのですが、16進数で$14$は$E$となるります。その点に留意すると、$3E8$が答えとなります。

他の進数の場合も割る値を$n$に代入してやれば同様にして求められます。

進数変換の計算問題

では慣れてきたところで一度練習問題を解いてみましょう。解法は上で説明した流れで解けるので、正答のみ記載します。

• 問1(10進数から2進数の計算)
• 問2(10進数から16進数の計算)
• 問3(2進数から10進数の計算)
• 問4(16進数から10進数の計算)

問1(10進数から2進数の計算)

問2(10進数から16進数の計算)

問3(2進数から10進数の計算)

問4(16進数から10進数の計算)

2進数・10進数・16進数まとめ

私達が馴染んでいる10進数以外を知らないと、試験で問われても答えられません。特に2進数・16進数は試験でもよく問われます。

基本情報技術者試験ではプログラミングと絡めた問題も出るので、浮動小数点やIPアドレスの計算とセットで理解しておきましょう。