[SPI・数学]推論:順列[無料問題集]

今回はSPIにおける順列の問題を解いていきましょう。


SPI順列の例題
SPIの順列では大抵複数人(4~5人)が登場し、条件が2~3個与えられた上で、誰が何番目かを求めるような出題がされます。
では早速SPI順列の例題を解いてみましょう。
問題1-1
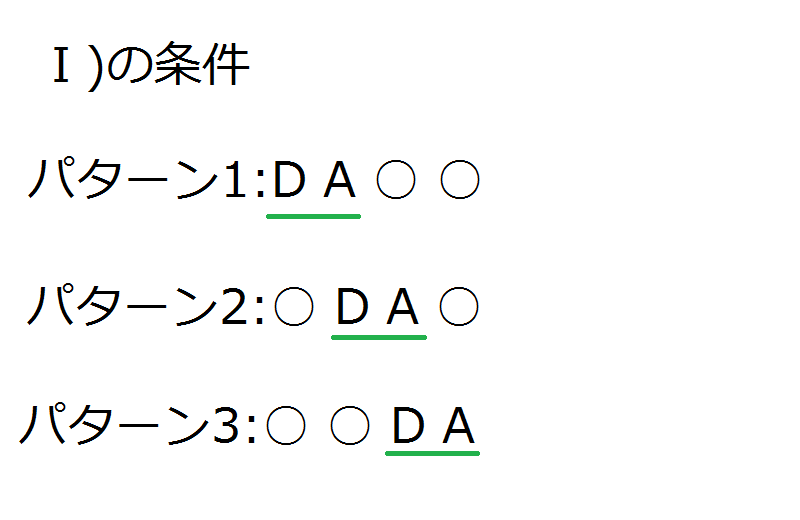
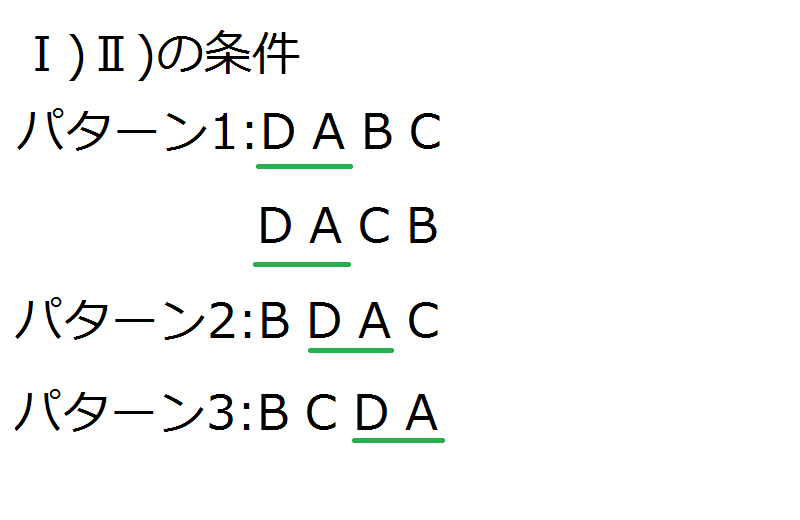
Ⅰ)Dの次にAがゴールした。
Ⅱ)Cは1位ではない。
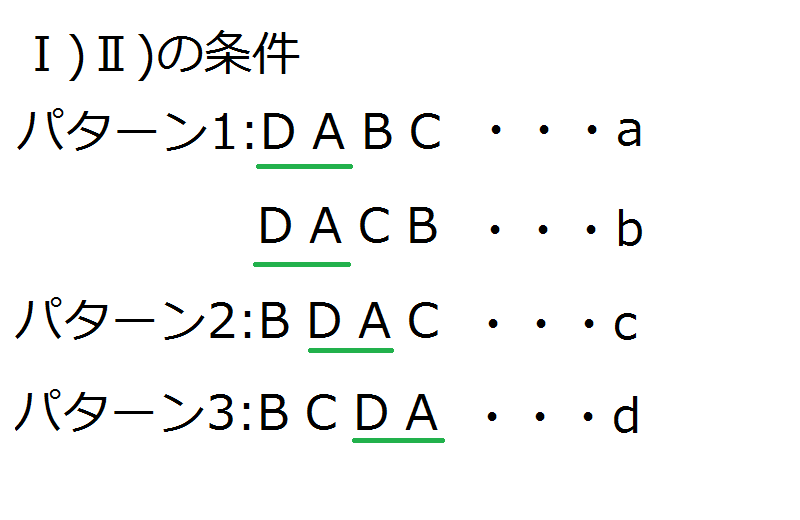
次の推論ア、イ、ウのうち、必ずしも誤りといえないものはどれか、当てはまるもの全て選べ。
ア:Bは2位である。
イ:Cは3位である。
ウ:Dは4位である。
(ログイン後回答すると、ここに前回の正誤情報が表示されます)
問題1-2
Ⅱ)Cは1位ではない。
4人の順位が全て分かるためには、Ⅰ)とⅡ)以外の情報で、次のⅢ)、Ⅳ)、Ⅴ)のうちどれが必要か。必要なものを全て選べ。
Ⅲ)Bより先にAがゴールした。
Ⅳ)Bより先にCがゴールした。
Ⅴ)Cより先にDがゴールした。
(ログイン後回答すると、ここに前回の正誤情報が表示されます)

問題2-1
Ⅱ)AはCよりも点数が高い。
Ⅲ)Bの点数はAとDの点数の平均である。
以上の条件より、4人の数学の試験の点数を高い順に並べたとき、Bの順位として考えられるものを全て選べ。
1位
2位
3位
4位
(ログイン後回答すると、ここに前回の正誤情報が表示されます)
問題2-2
A、B、C、Dの4人がそれぞれ、数学と理科の試験を受けた。この中で、数学の試験について、以下のことが分かっている。
Ⅰ)4人とも点数はバラバラである。
Ⅱ)AはCよりも点数が高い。
Ⅲ)Bの点数はAとDの点数の平均である。
このⅠ)~Ⅲ)の条件に加え、次の条件が加わった。
Ⅳ)Dの点数はCの点数より高い。
Ⅰ)~Ⅳ)の条件があるとき、次のア、イ、ウの中で数学の試験の点数について必ず正しいと言えるものを全て選べ。
ア:AはDより点数が高い。
イ:BはCより点数が高い。
ウ:BはDより点数が低い。
(ログイン後回答すると、ここに前回の正誤情報が表示されます)
問題2-3
Ⅱ)AはCよりも点数が高い。
Ⅲ)Bの点数はAとDの点数の平均である。
このⅠ)~Ⅲ)の条件に加え、次の条件が加わった。
Ⅳ)Dの点数はCの点数より高い。
Ⅴ)理科の試験の点数はAが最も高く、次いでCが2番目に高い。
数学と理科の合計点はBが最も高かった。このときのDの、数学と理科の試験の順位をそれぞれ答えよ。
数学
1位
2位
3位
4位
理科
1位
2位
3位
4位
(ログイン後回答すると、ここに前回の正誤情報が表示されます)
SPI順列のまとめ
SPIの順列では、部分的に固定して残った場所がどのような値をとりうるか推察します。
1つの値に絞られないことも多いので、選択肢のパターンはすべて試してみましょう。


福井県産。北海道に行ったり新潟に行ったりと、雪国を旅してます。
経理4年/インフラエンジニア7年(内4年は兼務)/ライター5年(副業)
簿記2級/FP2級/応用情報技術者/情報処理安全確保支援士/中小企業診断修得者 など





ディスカッション
コメント一覧
まだ、コメントがありません