[日商簿記1級]最小二乗法



経理の仕事をしていたり、簿記の勉強をしていたりするとたびたび統計の知識を求められることがあります。
これは、経理の仕事内容のひとつである、現在あるデータから未来を予測すると言った特性に由来しているものです。
その中でも個人的に苦手な方が多そうな最小二乗法についてご紹介します。
最小二乗法
最小二乗法は、主に工業簿記における原価計算で、いくつかのデータの合計の費用と作業時間が分かっていて、そこから変動比率と固定費を計算するための手法です。
そもそも最小二乗法とは、測定で得られた数値の組を、1次関数や対数関数など、特定の関数に近似するときにより正確な近似になるように、残差の二乗和を最小とするような係数を決定する方法です。
つまり、予想される関数f(x)=ax+bと各々の点の距離の二乗が最小になるようにする手法のことです。(下図の赤い線の長さの二乗が最小となる直線を求める。)
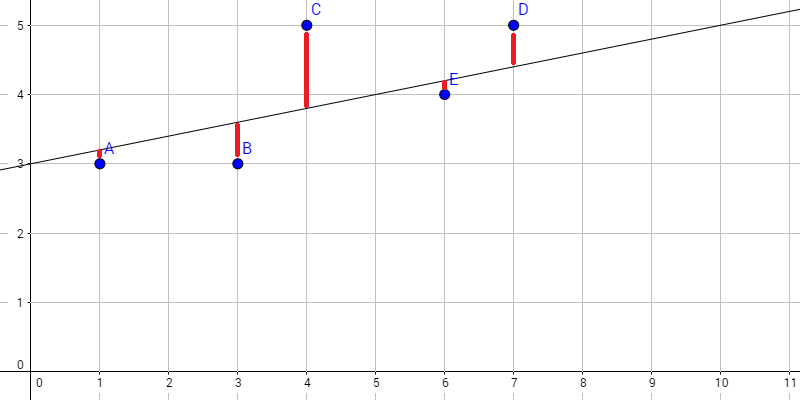
なぜ二乗するかというと、上図のように予想する関数f(x)=ax+bがあった場合、単純に直線と点との差の値を足していくだけだと、f(x)よりも下に位置するA、B、Eが負の値をとってしまい、正しい値が導き出せないからです。
では、早速その最小二乗法の求め方を見てみましょう。
\begin{eqnarray} \left\{ \begin{array}{l} \Sigma Y = a \Sigma X + n\cdot b \\ \Sigma X \cdot Y = a \Sigma X^2 + b \Sigma X \end{array} \right. \end{eqnarray}

この二次方程式を解けばいいのですが、なんだかややこしい式です。
しかし、記号の意味さえ分かってしまえば中学校で習う数学のレベルで十分解けます!
\Sigma(シグマ)ですが、数列のところでもよく見られる記号で総和を意味します。
※\Sigmaの由来としては英語で合計を意味するsumの頭文字Sが変形し、\Sigmaになったと言われています。余談ですが、積分を表す\int(インテグラル)もsumの頭文字が由来と言われています。

では早速、最小二乗法の解き方を具体的な例を通して学んでいきましょう。
問題
とある工場で直接作業時間(X)と、製造原価(Y)の実績記録があり、下記のとおりになっています。ここから製造原価(Y)変動比率のaと、固定費bに分けて、 Y = aX + bの形で表しなさい。
| 月 | 直接作業時間(X) | 製造原価(Y) |
| 4 | 800(時間) | 105,000(円) |
| 5 | 1,200 | 105,000 |
| 6 | 400 | 45,000 |
| 7 | 1,600 | 165,000 |
| 合計 | 4,000 | 420,000 |
解説
この問題は、連立方程式のそれぞれの項に正しい値を入れることが鍵です。
まず\Sigma Xと\Sigma Yですが、先ほど説明したとおり、\Sigma は総和をあらわします。つまり合計ということです。
したがって、上の表の合計の値を求めれば問題ありません。
\Sigma X = 4000、\Sigma Y = 420000
次にnの値ですが、このnはいくつサンプルがあるか、その個数を聞いているだけです。ここでは4~7月の4ヵ月分のデータがあるので、n = 4となります。
これで一つ目の式は、それぞれの値を代入すると420000 = 4000a + 4bとなります。
二つ目の式の\Sigma X \cdot Yと\Sigma X^2についても、改めて表を作ってみましょう。
| 月 | X | Y | X \cdot Y | X^2 |
| 4 | 800 | 105,000 | ||
| 5 | 1,200 | 105,000 | ||
| 6 | 400 | 45,000 | ||
| 7 | 1,600 | 165,000 | ||
| 合計 | 4,000 | 420,000 |
XとYの値は先ほどと変わらないので、そのまま転記すれば問題ありません。
次にそれぞれの月のX \cdot YとX^2を求めていきます。
4月の場合のX \cdot Yについて、\cdotは掛け算を表します。
X \times Yと同じ意味になるので、800 \times 105000 = 84000000となります。
5月以降も同様にその月の値を掛けていくと、以下のように表は埋まります。
| 月 | X | Y | X \cdot Y | X^2 |
| 4 | 800 | 105,000 | 84,000,000 | |
| 5 | 1,200 | 105,000 | 126,000,000 | |
| 6 | 400 | 45,000 | 18,000,000 | |
| 7 | 1,600 | 165,000 | 264,000,000 | |
| 合計 | 4,000 | 420,000 |
したがって、合計の値は以下のように求められます。
84000000 + 126000000 \\ + 18000000 + 264000000 \\ = 492000000
このことから、\Sigma X \cdot Y = 492000000が分かりました。
| 月 | X | Y | X \cdot Y | X^2 |
| 4 | 800 | 105,000 | 84,000,000 | |
| 5 | 1,200 | 105,000 | 126,000,000 | |
| 6 | 400 | 45,000 | 18,000,000 | |
| 7 | 1,600 | 165,000 | 264,000,000 | |
| 合計 | 4,000 | 420,000 | 492,000,000 |
次に\Sigma X^2です。これもまずは各月のX^2の値を求めていきます。
右上の小さい数字は二乗と言って、同じ数を2回掛ける意味です。4月、5月の例は以下の通りです。
- 4月:800 \times 800 = 640000
- 5月:1200 \times 1200 = 1440000
合計の値も含めて表にまとめると以下のようになります。
| 月 | X | Y | X \cdot Y | X^2 |
| 4 | 800 | 105,000 | 84,000,000 | 640,000 |
| 5 | 1,200 | 105,000 | 126,000,000 | 1,440,000 |
| 6 | 400 | 45,000 | 18,000,000 | 160,000 |
| 7 | 1,600 | 165,000 | 264,000,000 | 2,560,000 |
| 合計 | 4,000 | 420,000 | 492,000,000 | 4,800,000 |
これによって\Sigma X^2 = 4800000が分かります。そこで、連立方程式の二つ目の式に代入すると、以下のように求められます。
492000000 = 4800000a + 4000b
したがって、初めの数式は以下のように置き換えられます。
\begin{eqnarray} \left\{ \begin{array}{l} 420000 = 4000a + 4b \\ 492000000 = 4800000a + 4000b \end{array} \right. \end{eqnarray}
早速解いていくと、二つ目の式が0が多くて消せそうなので、両辺を1000で割り、
\begin{eqnarray} \left\{ \begin{array}{l} 420000 = 4000a + 4b \\ 492000 = 4800a + 4b \end{array} \right. \end{eqnarray}
とします。
一つ目の式と二つ目の式で4bが共通してあるため、二つ目の式から一つ目の式を引き算し、72000 = 800a、両辺を800で割り、a=90が得られます。
今度、この値をどちらかの式に代入してbを求めたいので、一つ目の式420000 = 4000a + 4bに代入します。
420000 = 360000 + 4b
60000 = 4b
b = 15000
より、b = 15000が得られました。したがって、変動費率a=90、固定費b = 15000となり、答えはY = 90X + 15000となります。
正答
最小二乗法・まとめ


最小二乗法は経理や簿記で求められることは多く、\Sigma のように意味を知らないと分からないこともあります。
しかし、意味さえ分かっていれば簡単に解けてしまうので、難しそうと身構る必要はありません。
次回も経理や簿記に必要な数学の知識の一つ、線形計画法についてご紹介します。

福井県産。北海道に行ったり新潟に行ったりと、雪国を旅してます。
経理4年/インフラエンジニア7年(内4年は兼務)/ライター5年(副業)
簿記2級/FP2級/応用情報技術者/情報処理安全確保支援士/中小企業診断修得者 など

 HELP
HELP


ディスカッション
コメント一覧
まだ、コメントがありません